¡Muy buenas a todos gente!
A continuación os dejo la solución al problema 3: la carrera más igualada del mundo, el cual seremos capaces solucionar haciendo uso de los conceptos de potencia e inversión los cuales estoy segurísimo que domináis a la perfección.
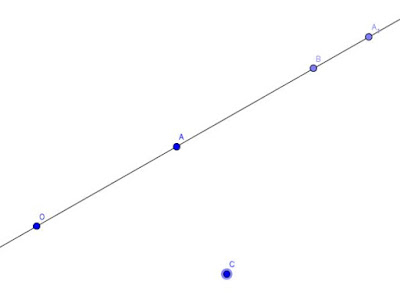
Deducimos que se trata de un caso de inversión porque si somos un poco perspicaces, que lo somos... nos daremos cuenta de que la condición para hallar la posición de Bruno no es otra cosa que la potencia de inversión, por tanto el ejercicio trabaja el concepto de potencia, en el que está basado la inversión. Además, si nos fijamos bien en nuestro problema podemos distinguir los distintos elementos de la inversión, un centro de inversión 0, dos puntos normales A y B y el inverso A1 colocados en la recta que une el centro 0 con el punto A original. Por tanto, es innegable que se trata de un problema de inversión, el cual vamos a solucionar mediante el siguiente procedimiento:
- Representamos un punto auxiliar C cualquiera:
- Tenemos
que hallar primero el inverso de C (Es decir, C1) Para ello hallamos la
mediatriz del segmento AC y la mediatriz del segmento AA1, y donde se crucen
ambas mediatrices tendremos el centro de la circunferencia que pasa por A, A1 Y
C, y obtendremos el punto C1:
- Unimos C1 con B
- Trazamos las mediatrices de CC1 y BC1 obteniendo así el punto I
- Con centro el punto I donde se encuentran las mediatrices, trazamos
una circunferencia que pasa por C, C1 y por B, obteniendo el punto buscado B1.
En la siguiente imagen podemos modificar algunos de las posiciones iniciales de los puntos (corredores) y de esta forma vemos que de una forma o de otra esta carrera inevitablemente acabaría en empate, ya que la potencia es constante y siempre se cumplirá que:
0A x 0A1 = 0B x 0B1
Con esto me despido hasta el siguiente problema.
That's all Folks!!!